雪崩光电二极管冲击电离事件空间分布的非局部模型

雪崩光电二极管冲击电离事件空间分布的非局部模型

2022年3月8日

下载版本

David A. Ramirez, Majeed M. Hayat，新墨西哥大学电子与计算机工程系和高技术材料中心;

Andrew S. Huntington, George M. Williams, 亚博棋牌游戏Allegro MicroSystems

本文基于:D. A. Ramirez, M. M. Hayat, A. S. Huntington和G. M. Williams，“雪崩光电二极管冲击电离事件空间分布的非局部模型”，载于《IEEE光子学技术通讯》第26卷第26期。1, pp. 25-28, 2014年1月1日，doi: 10.1109/LPT.2013.2289974。IEEE©2014。本材料允许个人使用。在任何当前或未来的媒体中，所有其他用途都必须获得IEEE的许可，包括为了广告或促销目的而复制/重新发布本材料，创建新的集体作品，转售或重新分发到服务器或列表，或在其他作品中重用本作品的任何版权组件。

摘要

解析死空间乘法理论的一个扩展。电工实习。《开发》第39卷，第546-552页，1992]。这个扩展提供了在任意指定的异质结倍增区域内解析确定电子和空穴冲击电离事件的空间分布的方法。该模型可用于理解死区在规范撞击电离位置中的作用。它还可以用于分析、设计和优化新一代具有多级增益的超低噪声雪崩光电二极管，基于适当的载流子激励和松弛，以增强电子冲击电离和抑制空穴冲击电离。

简介

雪崩光电二极管(apd)广泛应用于高数据速率光纤通信和激光雷达系统中，其工作波长为1.3 μ m。在APD结构中，独立吸收、电荷和倍增(SACM) InP-InGaAs APD一直是首选结构，原因有二。首先，它们具有高灵敏度，这是由于它们内部的载流子倍增，即由每个光生载流子产生的冲击电离雪崩。其次，与使用光学预放大的接收器相比，它们具有很高的成本效益。然而，由于冲击电离过程的随机性质，乘法增益以额外的噪声为代价。这种乘法噪声的特征是一个称为“超额噪声因子”的量，它解释了增益的不确定性。

人们已经探索了各种方法来降低apd的过量噪声因子。这些方法包括使用薄倍增区和冲击电离工程(I²E)乘法地区。这两种方法都利用了死区效应，通过使撞击电离的空间分布更加确定来减少多余的噪声。^{[1], [2]}死区是载流子必须经过的最小距离，它才能从电场中获得足够的能量，从而造成撞击电离。另一种方法是抑制空穴(或电子)的冲击电离，β→0(或α→0)，使α和β尽可能不相似。根据局域场理论，当其中一个电离系数远大于另一个时，apd的增益带宽积和超额噪声都会得到改善。^{[3], [4]}因此，人们对通过倍增区冲击电离工程抑制空穴(或电子)冲击电离的APD结构越来越感兴趣。^{[5], [6]}在这些结构中，一种载流子的弛豫(防止其冲击电离)是通过合理地设计异质结倍增区的不同层及其电场剖面来实现的。成功设计多层倍增区域的一个关键因素是能够准确确定电子和空穴触发冲击电离事件的位置。

本文报道了解析死空间乘法理论(DSMT)的一种扩展。^[7]这样就可以在任意指定的异质结倍增区域内确定冲击电离事件的空间分布。报告的递归方程允许在乘法区域的任何子区域内分别确定电子和空穴冲击电离事件的数量。此外，该模型可以考虑载流子弛豫，可以用来抑制一类载流子的冲击电离。

模型

考虑一个从x = 0扩展到x = w的任意乘法区域。由导电带电子引发的冲击电离事件称为electron-ionization事件；受价带空穴影响的冲击电离事件称为空穴电离事件。目标是计算单个父载波(在指定位置)启动雪崩过程后在子集中发生的电子电离事件和空穴电离事件总数的平均值。如果这个问题可以在任意子集A上解决——其中A是区间[0,w]的任意子集——那么它就可以特化为区间A₁= [0, w/n)， A₂= [w/n, 2w/n)，…，A_n= [(n - 1)w/n, w]，可以得到电子电离事件和空穴电离事件在整个倍增区的分布。(选择分区参数n以获得所需的空间分布分辨率。)为了解决这个问题，Z_e(x)和Z_h(x)分别定义为位置x处由父电子触发雪崩过程时电子冲击电离事件和空穴冲击电离事件的总随机数_e(x)和Y_h(x)分别定义为位置x处由父空穴触发雪崩过程时电子冲击电离事件和空穴冲击电离事件的总随机数。

递归方程的公式，使量Z的集合平均_e(x)和Z_h(x), Y_e(x)和Y_h(x)需要了解从载流子出生地点到其后第一次撞击电离地点的距离的概率密度函数。按照Hayat等人的符号，^[２]h_e(ξ|x)表示从x处电子出生位置测量到第一次电离的距离，ξ的概率密度函数;同样的,h_h(ξ|x)表示在x处产生的孔在第一次电离之前所经过的距离的概率密度函数。在DSMT中，h_e(ξ| x)和h_h(ξ|x)由移指数模型描述:

方程1:

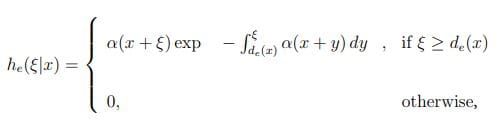
而且

方程2:

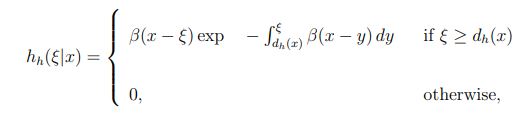
在维_e(x)和d_h(x)分别为电子死区和空穴死区。计算死区的精确公式可以在Hayat等人的工作中找到。^[２]

接下来，调用一个更新参数，类似于Hayat等人介绍的，^[8]得到量Z的均值的递归(积分)方程_e(x)和Z_h(x)， Ye(x)和Y_h(x)，记为z_e(x)和z_h(x) ye(x)和y_h分别(x)。考虑x处的父电子开始雪崩过程，并假设它的第一次电离发生在ξ值为> x的某个位置。

如果假设(暂时)ξ ξ A，则假设第一次电离发生在ξ，则Z的条件均值_ex就是z_e1(ξ)+ z_e2(ξ)+ y_e(ξ),z_e1(ξ)和z_e2(ξ)是ξ处两个子电子产生的总平均电子电离事件，而ye(ξ)是ξ处子空穴产生的总平均电子电离事件。另一方面，如果第一次电离的位置ξ值在A，那么在第一次电离的情况下，已经发生了一个电子电离，必须考虑这个额外的电子电离。这里是Z的条件均值_ex = 1 + z_e1(ξ)+ z_e2(ξ)+ y_e(ξ)。如果母电子不碰撞电离[概率为∞∫whe (ξ|x) d]，则Z_e(x) = 0。当考虑所有这些情况，并对第一个碰撞电离位置(由母电子)的所有可能位置ξ取平均值时，可以用简化法得到积分方程:

方程3:

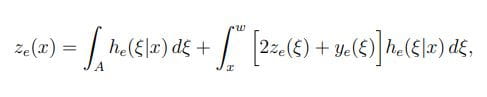
其中第一项只是第一次电离发生在区域a的概率。同样的论点可以重复分析量Z_h(x), Y_e(x)和Y_h(x);这样的分析导致了三个额外的积分方程:

方程4:

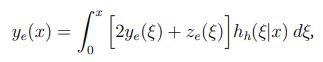
方程5:

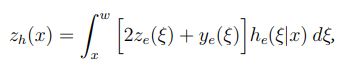
而且

方程6:

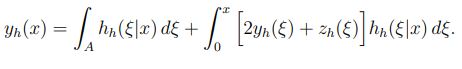
这些耦合递归方程(方程3、方程4、方程5和方程6)可以用一个简单的迭代方法进行数值求解。

结果

计算了两种不同倍增区的电子电离和空穴电离事件的空间分布:1)p同结倍增区的空穴注入;2)电子注入异质结倍增区。使用划分参数n，其中同质结乘法区域n = 50，异质结乘法区域n = 100。

计算得到的恒定电场作用下InP同构结倍增区150 nm内电子和空穴的冲击电离事件空间分布如图1所示。假设在x = 0处注入父孔。从图中可以看出，当空穴接近x = 150 nm时，空穴冲击电离事件数增加，当电子接近x = 0时，电子冲击电离事件数增加。这一结果与空穴和电子在相反方向运动时从电场中获得足够的动能而倍增的事实是一致的。更重要的是，该图显示了死区对冲击电离事件空间分布的影响。

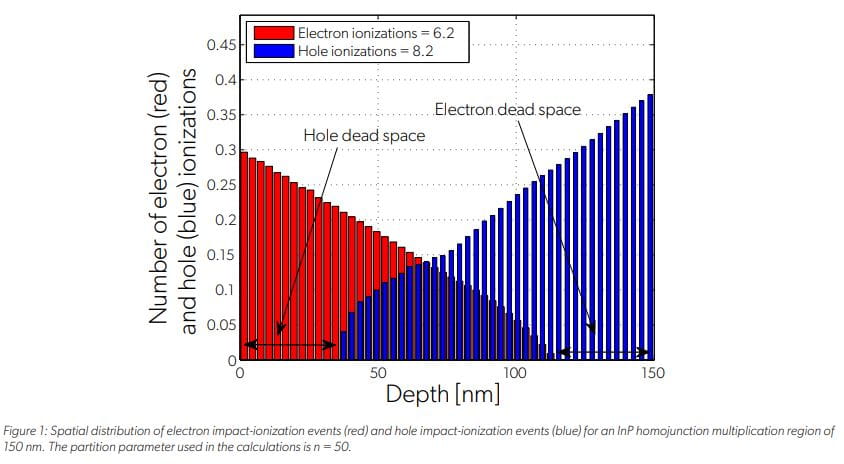
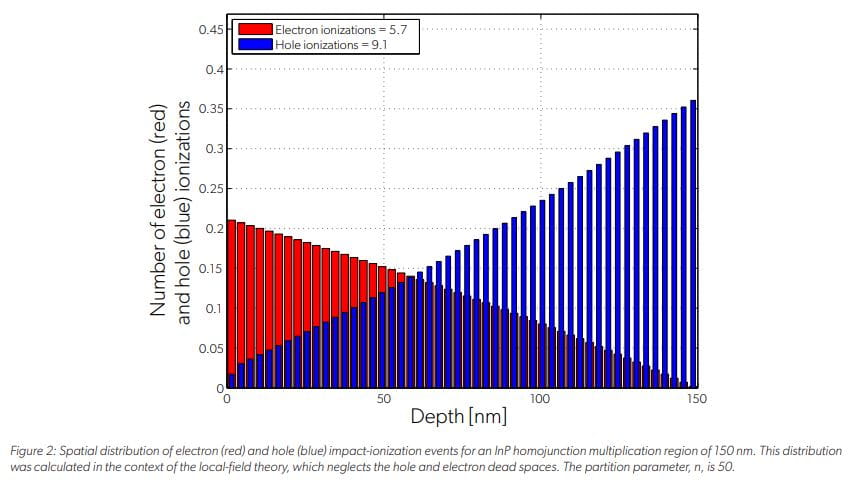
从x = 0到x≈37 nm的乘法区域开始的距离，其中空穴不发生冲击电离，对应于空穴死区的长度。在这部分的倍增区，空穴没有获得足够的能量来引发撞击电离事件。同样，乘法区域末端的距离——从x≈112 nm到x = 150 nm，在这一区域内电子不发生碰撞电离——对应于电子死空间的长度。图2在忽略死区的局域场理论背景下，比较了电子和空穴引发的碰撞电离事件的计算空间分布。从图2可以清楚地看出，局域场理论没有捕捉到死空间对冲击电离事件局部化的影响。这一结果的一个重要含义是，局域场理论不能正确预测薄乘法区(< 400 nm)的过量噪声因子，其中死区占乘法区的很大一部分。具体来说，众所周知，局域场理论高估了薄apd的过量噪声因子。例如，对于考虑的平均增益为15的乘法区域，DSMT预测的计算出的超额噪声因子约为5.4，而局域场理论预测的超额噪声因子约为10.5。

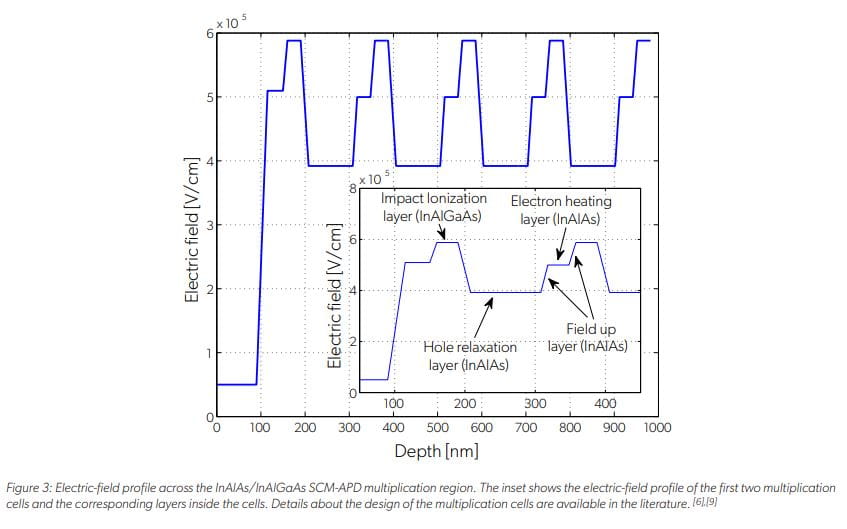
计算了具有InAlAs/InAlGaAs倍增区单载流子倍增(SCM) APD的电子和空穴冲击电离事件的空间分布。SCM apd是由Allegro光子学小组(当时作为Voxtel操作)开发的，通过抑制空穴引发的冲击电离事件来获得准确定性的倍增增益。^{[6], [9]}单片机APD的倍增区由级联倍增器结构组成，它结合了各种设计技术来抑制空穴引发的电离和增强电子引发的电离。^{[6], [9]}穿过乘法区域的电场剖面如图3所示。该倍增区有五个倍增单元，每个倍增单元由雪崩层、空穴弛豫层和电子加热层组成。图3的插图中显示了前两个倍增单元和单元内相应层的电场分布图。假设母电子在x = 0时被注入。孔洞弛豫机理的模型由Williams等人描述。^{[6], [9]}

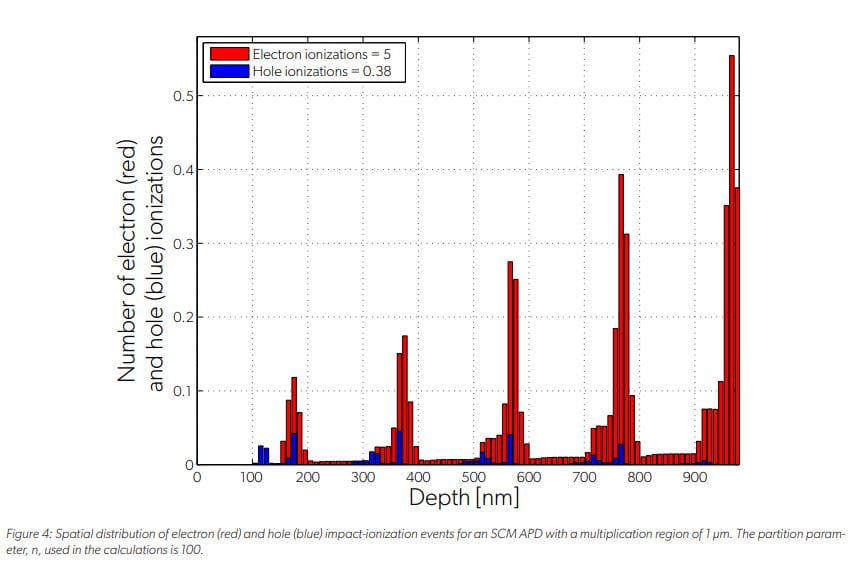
电子和空穴电离事件在乘法区(图3)的分布如图4所示。图中显示了低带隙和高电离率层(InAlGaAs)的冲击电离事件，这是电场达到最大值的层。图中还显示了电子冲击电离数与空穴冲击电离数之间的巨大差异。这种差异是由两个因素造成的:1)空穴弛豫层，它阻止空穴获得足够的动能进行冲击电离，从而减少多余的噪声;2)电子，在注入InAlGaAs层之前对其进行预热。这些结果与Williams等人报道的Allegro模拟结果一致。^[9]

结论

这里提出的解析递归模型能够分别确定电子电离事件和空穴电离事件的分布，因为雪崩过程是由父空穴或乘法区内任意位置的电子触发的。该模型可以模拟一种抑制由一种载流子触发的冲击电离的机制，从而能够确定单个载流子对局域冲击电离的影响。新模型是理解、设计和优化新一代apd的关键分析工具，旨在通过增强电子的冲击电离而抑制空穴的冲击电离(或反之，视需要而定)实现超低噪声特性。

参考文献

^[1]王淑华、马芳芳、李旭东、司杜、郑旭东、孙旭东、小A. L.霍姆斯、J. C.坎贝尔。具有中心阱倍增区域的超低噪声雪崩光电二极管。量子电子。2003年,39岁。

^[２]m.m. Hayat, O-H。权，S.王，J. C.坎贝尔，B. E. A.萨利赫，M. C.泰奇。薄型异质结构雪崩光电二极管中倍增噪声的边界效应:理论与实验。IEEE反式。电子学报，32(6):673 - 673,2002。

^[3]陈志强，“雪崩光电二极管的材料研究”，《量子电子学报》，第14期，2008年。

^[4]Joe C. Campbell，“电信雪崩光电二极管的最新进展”，《光波技术杂志》，25:109-121,2007年1月。

^［5］孙伟，郑晓霞，吕振华，“InAlAs/InAlGaAs串联雪崩光电二极管的蒙特卡罗模拟”，《电子学报》，29(1):52 - 56。

^[6]g.m. Williams, M. Compton, D. A. Ramirez, M. M. Hayat和A. S. Huntington，“多增益级InGaAs雪崩光电二极管增强增益和降低过量噪声”，电子器件学会学报，第1卷第1期。2, pp. 54-65, 2013年2月，doi: 10.1109/JEDS.2013.2258072。

^[7]M. M. Hayat, B. E. A. Saleh和M. C. Teich，“死空间对双载流子倍增雪崩光电二极管增益和噪声的影响”，IEEE Trans。电子学报，39:546-552,1992。

^[8]M. M. Hayat, W. L. Sargeant和B. E. A. Saleh，“死空间对Si和GaAs雪崩光电二极管增益和噪声的影响”，《IEEE J.量子电子》。1992年,28:1360 - 1365。

^[9]g.m. Williams, M. Compton, D. A. Ramirez, M. M. Hayat和A. S. Huntington，“通过非对称载波调制实现增加增益的InGaAs雪崩光电二极管，”《应用物理学报》，已接受，2013年。