使用超过阈值时间进行距离-步行校正

使用超过阈值时间进行距离-步行校正

2021年8月19日

George M. Williams, Jr.， All亚博棋牌游戏egro MicroSystems

下载版本

简介

飞行时间激光雷达系统基于脉冲返回上升沿通过检测阈值的过渡来测量脉冲返回到达时间。这些系统受制于系统距离误差，称为范围内走对于两个原本相同但振幅不同的脉冲返回，且都强到足以超过一个固定的检测阈值，较弱脉冲返回的上升沿将在比较强脉冲返回的上升沿更接近脉冲中心的时间越过阈值。

由于距离步进是一个系统误差，而且距离步进是脉冲返回幅值的单调函数，因此可以根据脉冲返回幅值的测量进行校正。

然而，在大多数激光雷达应用中，脉冲返回振幅的动亚博尊贵会员态范围超过了光电接收器的电子动态范围，导致信号饱和。

一种简单的替代方法是使用超过阈值时间度量。超过阈值的时间——脉冲返回的上升边缘和下降边缘通过探测阈值之间的时间——与脉冲振幅单调相关，但更容易测量。

本文表明，在大于90 dB的脉冲返回动态范围内，基于时间阈值测量的查找表或多项式校正可用于将基于雪崩光电二极管的激光雷达系统的范围走动减少到±0.2米以内。

背景

飞行时间激光雷达系统测量到目标的距离是基于纳秒级激光脉冲由激光雷达传输并由目标反射回激光雷达的往返旅行时间(图1)。

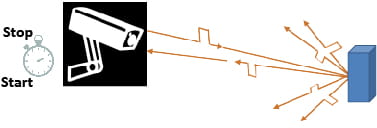
图1:飞行时间激光雷达的基本原理:激光雷达记录飞行时间，这是当它检测到发射激光脉冲的传输和接收反射目标返回之间的间隔。然后将飞行时间转换为一个使用光速的范围。

基于雪崩光电二极管(APD)的激光雷达光电接收电路如图2所示。在这种接收器中，APD将光信号转换为光电流脉冲，低噪声跨阻抗放大器(TIA)将电流脉冲转换为电压脉冲。然后，阈值比较器将模拟电压脉冲转换为数字信号，该数字信号可由时间-数字转换器(TDC)计时。

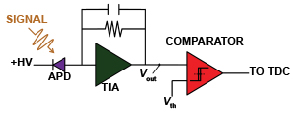
图2:基于apd的激光雷达光接收机框图。(+HV为APD高压反向偏压，V_出是TIA输出的模拟电压信号，V_th为检测阈值;V_出与V相比较_th．)

在理想情况下，飞行的物理时间(τ)是传输的激光脉冲的中心(T₀)和目标反射中心(T_停止)：

方程1:

τ= T_停止- T₀[s]。

目标距离(R，单位为米)是从τ和空气中的光速(与真空中的光速(c，单位为m/s)相同)计算到大约万分之一的范围内:

方程2:

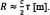
飞行时间方法的错误

与理想情况相反，测距测量受到系统误差和随机误差的影响，系统误差可以通过校准来校正，而随机误差则不能。系统误差导致距离精度的丧失，随机误差导致距离精度的丧失。^[1]

随机无法改正的错误

与τ的系统误差相反_抵消， APD和TIA中的随机过程都会导致τ的值_抵消即使平均脉冲振幅和检测阈值是恒定的，它也会在一组相同准备的测量值上波动。因为每次测量的波动幅度是随机的，它不能通过校准去除。

随机定时误差来自于APD和TIA叠加在进入激光雷达比较器的上升信号脉冲上的高频振幅噪声，如图3所示:对于任何给定的测量，进入比较器的噪声信号向上波动会使信号跨越检测阈值的时间提前，向下波动则会延迟脉冲被检测的时间。在一组相同准备的测量中，高频振幅噪声的大小由阈值跨越平均时间时信号振幅的标准差(σ)量化_n)．上升信号在过阈值时刻的平均斜率(dV/dt)将高频振幅噪声转化为定时抖动(σ)_t)，它是脉冲探测时间在一组测量值上的标准差。

抖动不能通过校准去除，因为每次测量的噪声波动的幅度是随机的。

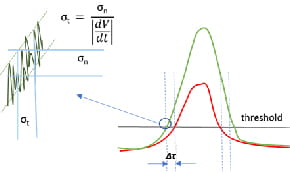
图3:Jitter (σ_t)是一个随机错误，因此是不可纠正的。抖动是由高频振幅噪声(σ_n)叠加在信号脉冲上。在阈值处上升的平均信号脉冲(dV/dt)的斜率变换为σ_n在σ_t．与抖动不同的是，单个脉冲(Δτ;为阈值跨越时间随信号脉冲幅值变化而产生的系统误差，因此是可修正的。

显然，既需要高精度又需要高精度的测量。在实践中，激光雷达系统被设计成最小化导致不精确的随机误差，然后校准以消除导致不精确的系统误差。接下来介绍消除系统距离行走误差的方法。

系统错误(矫正)

根据公式2，有一种系统误差很容易理解，它假设激光雷达系统和目标之间光程中的光速完全等于真空中的光速。这一假设引入了一个系统误差，如果路径上的平均群折射率(n)是已知的，就可以消除该误差——这取决于大气压力、温度和湿度等环境因素:

方程3:

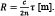
距离误差是另一种类型的系统误差，它取决于脉冲返回振幅。由于对于给定的激光雷达系统和目标，脉冲返回振幅随exp(-2σR) R的变化而变化，因此使用距离步长来表示与振幅相关的误差²对于大于投影激光光斑的面积目标，为exp(-2σR) R⁴对于小于投影激光光斑的面积目标，σ为m-1的大气衰减系数。因此，这种类型的距离误差本身就是距离的函数。^[２]

由于距离移动造成的距离精度误差来自于图4所示的脉冲定时。而τ是发射(开始)和反射(停止)脉冲中心之间的时间间隔₀和T_停止)，对于如图2所示的光接收器电路，脉冲的计时取决于前缘何时过渡到检测阈值(时刻T_0,和T_停止,)．抵消ΔT₀ΔT_停止在各自脉冲的中心之间，以及当脉冲被接收电路检测到时，结合起来产生偏移飞行时间测量(τ_抵消)．定时偏移有系统地依赖于脉冲幅度和检测阈值，因此产生的距离误差也是系统的，因此是可以修正的。

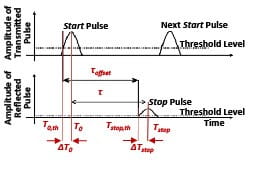
图4:使用前沿探测器的激光雷达系统测量飞行偏移时间(τ_抵消):物理飞行时间(τ)被取决于发射和反射脉冲振幅的时间间隔所抵消。这些时间间隔，ΔT₀ΔT_停止，也取决于用于计时的检测阈值。

物理飞行时间(τ)与测量的飞行偏移时间(τoffset)相关:

方程4:

τ=τ_抵消+Δτ[s],

其中总系统误差Δτ为:

方程5:

Δτ=ΔT_停止-ΔT₀[s]。

与起跑(T₀)或停止_停止)的脉冲如图3所示，其中两个形状相同但振幅不同、峰值同时出现的脉冲叠加在一起。与定时抖动一样，信号水平的向上移动会导致脉冲的前沿提前越过检测阈值。然而，与抖动不同的是，向上的位移是激光脉冲振幅的结果，而不是随机波动，因此定时偏移是系统的。同样，对于恒定振幅的返回信号，改变阈值从低电平到高电平，会导致系统的距离-走差误差，该误差随着阈值接近脉冲振幅而减小。

纠正系统距离-行走误差

在实际的激光雷达应用中，信号幅值相对于亚博尊贵会员检测阈值水平的变化，作为目标距离、目标大小和目标反射率的函数，将导致系统距离误差。

对于使用前沿脉冲探测的激光雷达系统，导致距离偏移的定时偏移与脉冲振幅成正比，且具有确定性——这意味着如果脉冲振幅可以测量，且脉冲振幅和定时偏移之间的定量关系已知，则可以通过校准去除这些偏移。

从25 m到25 km范围内的目标返回到21 mm口径激光雷达系统输入的激光脉冲回波信号幅值模型如图5所示。从激光脉冲离开发射机的时间到脉冲从最近的目标(0米)和最远的可探测目标(约25公里)返回的时间，信号振幅变化显著。在本例激光雷达系统的全灵敏度范围内，信号振幅变化大于90 dB。

图5:对于0米到25公里的目标距离，计算得到的信号返回振幅变化约90 dB。

理想情况下，孔径参考检测阈值水平与信号幅值保持固定比例，这样脉冲幅值与阈值水平的比值在起始时间(T₀)为脉冲振幅与停止时阈值水平的比值(T_停止)．

不同振幅的单回激光脉冲(T₀或T_停止)如图6所示，其中覆盖了峰值振幅在0.1到1个任意单位(AU)之间变化的7纳斯半最大(FWHM)全宽高斯脉冲。为了简单起见，这里假设APD和TIA具有无限的带宽，并且能够再现理想的高斯激光脉冲。如图所示，当检测阈值固定在0.1 AU时，可能会产生高达7 ns的距离-走差误差。

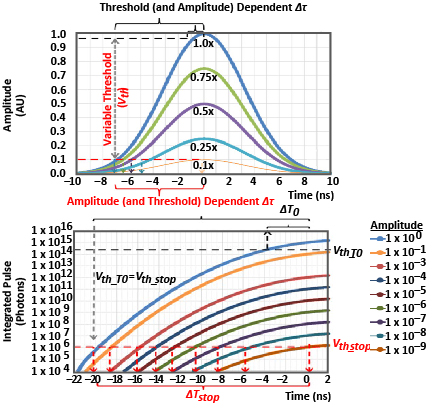
图6:如果使用固定的检测阈值，即使信号幅值的10分贝变化也会导致7 ns的FWHM高斯脉冲的时间偏移(上)。原则上，在这种情况下，一个时变阈值可以纠正多达20 ns的偏移量。

图6底部显示了一个较宽信号振幅范围的例子。在本例中，假设TIA具有对信号脉冲进行积分的能力。在这个例子中，其信号动态范围接近于图5所示的模型，在低阈值水平下操作的光电接收器检测到大信号返回时，距离-行走误差可高达20纳秒。根据公式3,20ns的计时误差将导致3米的距离精度误差。对于固定阈值探测系统，这样的误差是不可避免的，因为阈值探测器是用来感知出射激光脉冲和从最远的可探测目标返回的激光。

在激光雷达系统中，有几种方法可以减小系统距离误差。这些方法包括操作方法，如时变阈值和校准方法，如时间超过阈值;这些方法可以单独使用，也可以一起使用，以提高射程精度。

时变阈值

因为信号返回振幅随范围的系统变化与exp(-2σR) R之间的范围成正比⁴和exp(2σR) R²，距离行走误差本身是距离的函数。因此，从原理上讲，可以随着时间改变检测阈值，从而跟踪信号返回振幅的总体趋势，从而减小距离-行走误差。

在具有时变阈值的激光雷达系统中，检测阈值(V_th)在量程测量过程中从初始高值(V_{th_T0})的最小值，导致可接受的假报警率(V_{th_stop})．V的变化_th从V_{th_T0}到V_{th_stop}当发出的激光脉冲被传输时开始，Vth的变化率被控制，因此，理想情况下，V_th保持与信号返回振幅的恒定比例，直到V_{th_stop}是达到了。在图6所示的情况下，底部如果V_th在整个信号返回范围内，完美地跟踪信号返回振幅，20纳秒的距离行走误差可以减少到接近0纳秒。

然而，难以解释信号返回振幅的距离依赖性，它随目标的大小和方向等属性以及当地的大气条件而变化;这阻止了单一的时间相关阈值函数的普遍适用。下面讨论时变阈值的几个限制。

1. 信号返回振幅与目标距离匹配:设计一种阈值调节电路，使信号返回振幅衰减与目标范围平滑匹配，是一项具有挑战性的工作。通常，通过电阻放电的电容的指数衰减被使用，它有一个时间常数(τ_{钢筋混凝土})等于电阻(欧姆)和电容(法拉)的乘积:

方程6:

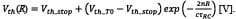
可以选择电阻和电容来调整τ_{钢筋混凝土}，但式6偏离了目标的指数衰减，一般在exp(-2σR) R之间²和exp(2σR) R⁴，因此剩余距离-步进误差与距离相关。

2.考虑到目标的大小和形状:由于激光束的发散，目标可以在近距离比激光光斑大，但在远距离比激光光斑小，这样不同大小的区域目标的信号返回振幅从R切换²依赖到R⁴不同范围的依赖性。如果目标是导线或其他一维目标，信号返回振幅以近似的R变化³依赖。

此外，由于当反射来自较近的目标时，阈值较高，如果阈值衰减设置不正确，在中程探测到目标的概率可能会降低

3.考虑目标反射率:除了大小和方向外，目标因反射率而异。对于同一距离的不同目标，目标反射率的变化导致信号返回振幅的变化。如果不加以纠正，这将导致距离行走误差。

4.考虑大气属性:由于灰尘或雾霾等物质的散射，衰减系数也随着大气条件的变化而变化很大。这将导致信号的指数衰减是大气衰减系数的函数。

5.有限的电子动态范围:使用时变阈值可以降低系统误差的信号幅值范围受阈值比较器动态范围的限制，该动态范围一般小于20 dB。

从根本上说，时变阈值方法假设信号返回振幅与目标距离之间存在相关性，但基于实际信号返回振幅测量的距离行走校正更为普遍。

时间阈值

时变阈值的挑战可以通过前沿脉冲检测来确定信号超过检测阈值的时间(时间超过阈值，TOT)来克服。

直接测量超过多个数量级的脉冲振幅具有挑战性。通常，一个有效的激光雷达光接收器需要一个具有高跨阻抗增益的TIA，以便它能对来自远处目标的微弱信号敏感。然而，当TIA增益较高时，较强的信号驱动TIA达到饱和。这显示在图7中绘制的光接收器的电路模拟集中，其中来自APD的输入光电流脉冲跨度从300 nA到1a，如上图所示。TIA输出电压(V_出)在信号的大部分动态范围内饱和于略高于1v，如图7所示(中间)。比较器转换的时机导致了很明显的距离走动，如图7所示，底部。由于TIA的模拟输出电平饱和，不能用于测量大部分信号动态范围内的脉冲幅度，因此需要一种使用激光雷达电路测量幅度的替代方法。

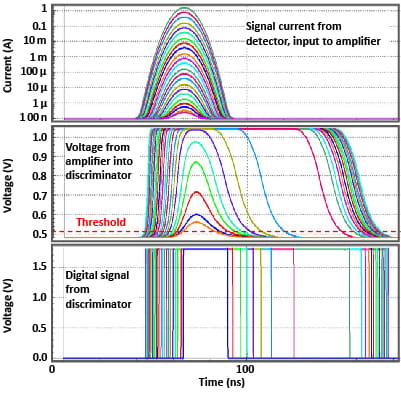
图7:信号变化大于90 dB的APD(上)、TIA(中)输出和阈值鉴别器(下)输出的电路模拟。

由于TIA饱和引起的脉冲幅值测量的挑战可以克服，因为即使TIA输出饱和，在这种TIA设计中，输出脉冲的宽度随着信号幅值呈单调关系增加，如图7所示(中间)。因此，激光雷达接收机的比较器可以根据TIA输出的上升和下降边缘的时序测量来推断脉冲振幅。由此产生的超过阈值的时间可以作为距离行走校正中脉冲振幅的替代品。从图7的模拟中测量的TOT数字脉冲宽度和距离游走(均以ns为单位)的计算被绘制为图8中脉冲振幅的函数。

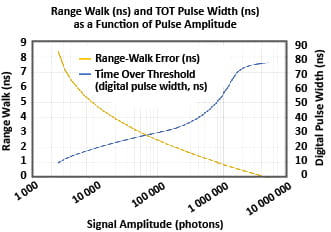
图8:距离-行走误差(主y轴)和超过阈值时间(次y轴)的模拟:图6中模拟的各种脉冲振幅测量了绘制的数据。

虽然查找表可用于任何接收器的距离行走校正，但分段线性或多项式函数拟合在确定偏移校正方面是有效的。图9显示了拟合图8中的距离-步行-偏移误差的六阶多项式;还绘制了脉冲幅值数据减去多项式校正后的残差。残差精度误差的标准差小于8 mm。

图9:剩余距离正时误差的模拟:剩余距离正时误差(二次y轴)是由距离步进的简单分段线性校正得到的，绘制为信号幅值的函数，与测量的原始时间步进(ns)相比。误差上的标准偏差对应大约3厘米的范围误差

前面的例子是使用模拟数据生成的。在实际应用中，激光脉冲的形亚博尊贵会员状不是高斯的。例如，被动调q激光器在发射主激光脉冲之前，经常发射数十纳秒的激光。这表明了基于特定应用需求对任何给定激光雷达系统设计的TOT特性进行经验校准的重要性。

在三个相同配置的飞行时间传感器上采集的现场数据，配置了一个Allegro 23 MHz APD光电接收器和一个Allegro 300 μ J被动q开关二极管泵浦固态激光器，如图10所示。使用不同反射率的目标在不同的范围内采集数据。给出了与数据拟合的五阶多项式。对数据进行多项式校正后的残差范围误差如图11所示。用相同的多项式函数对三种测距系统的数据进行校正后，距离数据在所有距离上的标准差都小于0.2米。我们的分析表明，大部分残留的距离误差是由于距离测量的精度和被动调q激光器上的抖动。

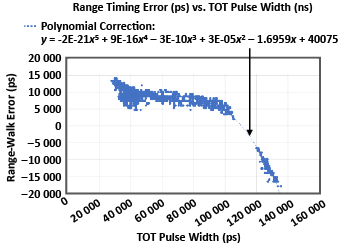
图10:距离测量中的误差(以皮秒为单位)作为从多个距离测量数据中提取的TOT脉冲宽度的函数。

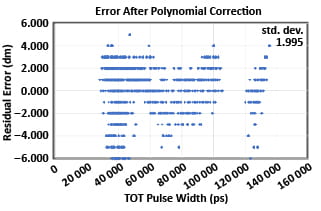
图11:多项式校正后的残余误差(分米)作为实测TOT脉冲宽度的函数。

结论

激光雷达系统中使用的前沿脉冲探测器存在随机误差和系统误差，分别导致距离精度和精度的损失。虽然一般只能通过增加返回脉冲幅度或平均多个脉冲来提高距离精度，但在距离测量中，称为距离游走的系统振幅相关误差可以减少。提出了两种校正系统距离行走误差的方法。

时变阈值降低了返回脉冲信号幅值与阈值水平之间的比值随距离的变化，从而降低了激光雷达对返回脉冲幅值变化的敏感性。然而，该技术在动态范围内受到限制，容易受到目标大小、形状和反射率变化以及大气效应的影响。

相比之下，与固定阈值一起使用或与时变阈值同时使用的时间超过阈值校准，允许减少系统距离-走差误差。

来自Allegro APD光电接收器的模拟数据已被用来证明系统误差是TOT的单调函数，并演示了TOT校准背后的原理。从现场测量中获得的数据表明，该系统能够将35纳斯(大于10米)的距离振幅依赖性行走误差校正到距离真实值0.2米以内。

^[1]精度一词是用来描述随机误差，如定时抖动。在这里，我们使用精度来指代系统误差，如距离误差，这是该术语最常见的用法。在这里的用法中，精度和精度是独立的，因此任何高或低的精度或精度的组合都是可能的。由国际标准化组织(International Organization for Standardization)建立的准确度一词的另一种用法包括相对于真实值的随机误差和系统误差。

^[２]非二维目标可以有其他信号关系。例如，导线可以有exp(-2σR) R³信号变化作为距离的函数。