激光雷达有效范围
2021年8月24日
激光雷达有效范围
2021年8月24日
小乔治·m·威廉姆斯著;安德鲁·亨廷顿。博士,快板亚博棋牌游戏微系统
简介
激光雷达系统的有效距离取决于其光接收机的灵敏度和返回光信号的强度作为目标距离的函数。讨论了影响信号返回强度的参数,包括激光脉冲能量、大气条件、目标的尺寸、方向和表面特性。
激光雷达的概述
自从激光出现以来,光探测和测距已被证明是测量距离最有用的方法之一。飞行时间(TOF)激光雷达技术采用了一种类似于早期雷达的方法,即使用短脉冲光而不是微波。TOF激光雷达系统包括一个发射纳秒级脉冲的激光发射器,一个检测并计时光脉冲的光接收器电路,以及将激光投射到目标上、收集后向散射光并将其聚焦到光接收器上所需的光学器件。根据真空中的光速(c)和激光雷达系统与目标之间光路的平均群折射率(n),利用发射出的激光脉冲的传输与目标反射的脉冲到达接收机之间的飞行往返时间(τ)来计算目标距离(R):
方程1:
R = (c/2n)τ [m]。
激光雷达系统的有效距离有限,因为后向散射光信号随着目标距离的增加而减弱,因此从非常远的目标返回的光接收器太弱而无法探测到。因此,激光雷达系统的有效距离取决于其光接收器的灵敏度和作为目标距离函数的光信号返回的强度。
例子:例子
为了比较各种参数对激光雷达距离性能的影响,除非另有说明,本文中所介绍的案例均采用表1中总结的示例案例。此外,在本文中还提到:overfilling (OF)靶是给定横截面积(通常为2.3 × 2.3 m)的靶2)在投射的激光光斑比目标大的范围内;欠填充(UF)目标是一个扩展的目标,如山坡或指定的横截面积的目标,其投射的激光光斑小于目标。
表1:实例的参数
| 参数 | 描述 | 价值 |
| 一个t | 目标截面积 | 2.3 x 2.3米2 |
| ϕ | 半角激光束发散 | 0.5 mrad |
| R的 | 超过这个范围,目标就会被过度填充 | 2.6公里 |
| Etx | 发射激光脉冲能量 | 300μJ |
| θ | 入射角 | 30° |
| ρ | 扩散反射率 | 30% |
| η | 光学系统的效率 | 90% |
| D | Receive-aperture直径 | 21毫米 |
| Nf | 实现特定FAR所需的因子 | 8 |
| NEI | 噪声等效输入 | 33 ph值 |
| λ | 激光波长 | 1534海里 |
| EPh值 | 光子能量(单位:焦耳) | 1.28 x10-19年J |
辐射模型
决定激光雷达系统有效范围的信号返回电平取决于光接收机的灵敏度和应用程序所容忍的最大假报警率(FAR)。激光雷达系统被设计为忽略弱于指定检测阈值的脉冲,以消除由光接收机噪声引起的假警报,但弱于检测阈值的光信号返回也被忽略。因此,激光雷达系统以所需的最小检测阈值操作,以实现略低于应用程序允许的最大FAR。检测阈值通常是接收机噪声的6到10倍。
对于平均信号水平等于检测阈值,检测概率(Pd)在相同制备的脉冲集合上的平均值为50%。根据光接收机输出的互补累积分布函数(CCDF),对于超过检测阈值的信号电平,检测概率增加。然而,Pd和具有检测阈值的FAR依赖于光接收器内部的细节。激光雷达有效距离的一般分析可以从以下理解出发:检测阈值是光接收机灵敏度的固定倍数,可能是6到10,检测阈值处的信号将以50%的概率被检测到。
光接收机灵敏度可根据光接收机输入处的概念光信号电平来量化,该电平将导致等于光接收机输出噪声幅度的平均输出电平。当以功率为单位测量概念光信号电平时,灵敏度由噪声等效功率(NEP)量化;如果信号电平以光子为单位表示,则可以指定噪声等效输入(NEI)。光接收机灵敏度是激光脉冲宽度、探测器工作温度的函数,对于基于雪崩光电二极管(APD)的接收机,是APD的雪崩增益的函数。
当接收机噪声表示为等效信号电平时,门限信号电平(Sth),以确定激光雷达的有效距离,可表示为:
方程2:
年代th_NEP= Nf× nep [w];或
方程3:
年代th_NEP= Nf× NEI[光子],
其中Nf是达到特定FAR要求所需的因子,通常在6至10之间。
鉴于年代th,辐射模型可用于确定激光雷达系统在特定条件下对特定目标接收的平均反射信号幅值。辐射模型与Sth得到了距离方程,根据发射激光脉冲、目标和介入大气的特性,给出了激光雷达系统的有效距离。
激光脉冲在大气中传播时被衰减,并可能因局部折射率变化而变宽、散焦,甚至偏离直线路径,这种局部折射率变化是由风和湍流引起的大气密度随时间的变化引起的。脉冲的衰减和扭曲程度取决于激光的波长和功率、穿过大气的光程长度以及大气的特征,如温度、能见度和湍流强度。
吸收和散射的综合效应可以用光功率(或脉冲能量)衰减系数(σ)(单位为m)来表征1.光束截面积内的激光通量(A梁)在m2,在射程内R以米为单位,可以近似为:
方程4:
F = (etx/一个梁) exp(-σR) = [Etx/π(ϕR)2] exp(-σR) [J m2),
在Etx其中,其中φ为发射激光脉冲能量,单位为焦耳,其中φ为半角激光束发散度,单位为弧度。
根据光束发散度、目标的大小和到目标的距离,投射到目标上的激光光斑可能:将目标下填充(图1,上),在这种情况下,激光脉冲中的所有能量都被目标散射;或过度填充目标(图1,底部),在这种情况下,只有一部分脉冲能量会被目标散射。在任何一种情况下,如果激光束以入射角θ撞击目标表面,进入目标表面的通量将减少cos(θ)的一个因素,因为投射到倾斜表面上的激光光斑延长了1/cos(θ)。然而,这只影响入射到目标上的总能量(G“透明国际”)在满的箱子里。
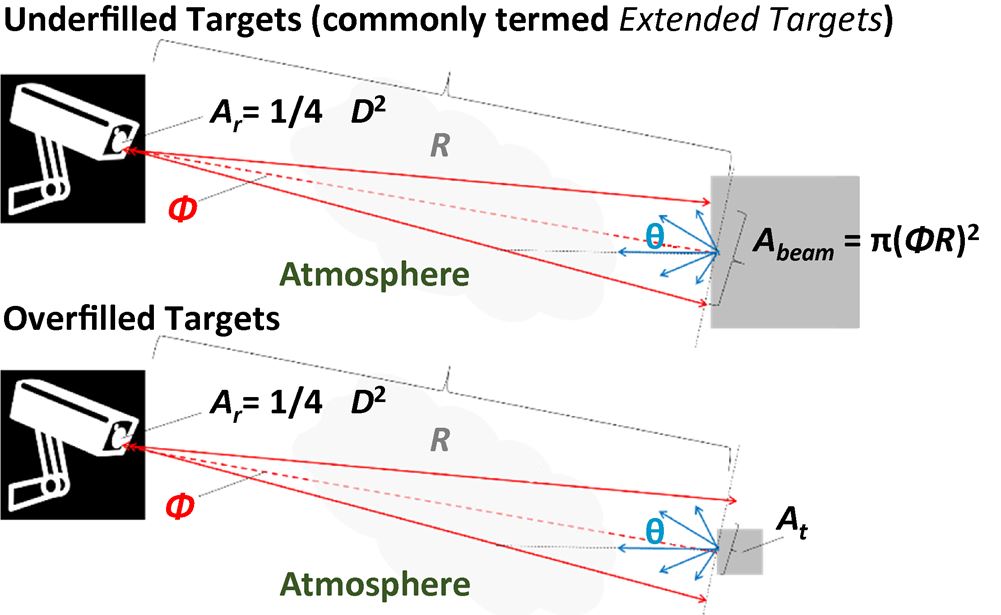
| 一个r | 接收口径截面积,单位为m2 |
| D | 接收口径以米为单位 |
| R | 到目标的距离,单位为米 |
| 一个梁 | 梁的横截面积,单位为m2 |
| Φ | 半角激光束发散弧度 |
| θ | 以弧度为单位的入射角 |
| 一个t | 目标截面积,单位为m2 |
图1:未填充目标的测距(大于激光光斑;顶部)和一个过度填充的目标(比激光光斑小;底部)
对于未填充目标(通常称为扩展目标);(图1,上),入射到目标上的能量为:
方程5:
Gti_UF= Etxexp (R -σ)[J]。
与激光入射角有关的cos(θ)因子在公式5中没有出现,因为激光光斑大小的变化与通量的变化相抵消。这可以用另一种方式来考虑:如果激光光斑包含在目标区域内,那么激光脉冲中100%的能量必须传递到未填充的目标表面。
对于一个过度填充的目标(图1,底部),入射能量是减少的通量和目标面积(At,用m表示2):
方程6:
Gti_OF=一个t因为(θ)[Etx/π(ϕR)2[J]。
另一种考虑公式6中的cos(θ)因素的方法是,被过填的目标拦截的激光脉冲能量的分数是目标投影到垂直于激光束的平面上的面积与该平面上的激光光斑面积的比率。投影到波束法向平面上的目标面积随cos(θ)而缩小。
式6不能自动保证目标被过度填充,当目标区域大于π(ϕR)时,由式6得到伪结果。2.同样地,公式5对于过度填充的目标也会给出错误的结果。为了确定要应用的正确方程,必须对目标进行建模,并确定在给定范围内是不足填充还是过度填充。尽管入射激光脉冲能量取决于目标物体所呈现的详细形状和方向,以及激光雷达系统的瞄准精度,但超过目标被过度填充的范围可以近似为:
方程7:
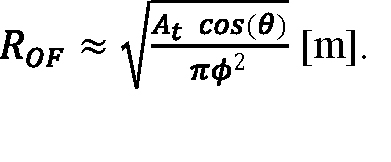
方程7中的cos(θ)因子解释了激光束中目标横截面的变化,模型为相对于光束轴倾斜的单个平面。然而,应该记住,真正的三维目标物体具有其他曲面,当其他曲面旋转出光束时,这些曲面将旋转入光束。(解释多个目标表面和方向的方法将在后面讨论。)
如果目标是一个以漫反射为特征的朗伯反射器(ρ),总反射能(Gtr)是:
方程8:
Gtr=ρ克“透明国际”[J],
在G“透明国际”是Gti_UF或Gti_OF是合适的。单位固体角的反射能随方向变化为:
方程9:
Gtr,Ω=[(ρG“透明国际”)/π] cos(θ′)[J sr .1),
θ′是相对于目标曲面法线的反射角。
请注意,π-而不是2π-出现在式9的分母上,因为cos(θ’)方向因子。如果微分表面元素- sin(θ´)dθ´dφ´在球极坐标中,其中θ´是天顶角,φ是方位角-在一个单位半球上进行积分,则半球的面积(2π)的结果。然而,如果微分面元乘以cos(θ´),结果是π。因此,如果Gtr,Ω在一个单位半球上积分,则总反射能量(Gtr=ρG“透明国际”)恢复正常,如预期:
方程10:
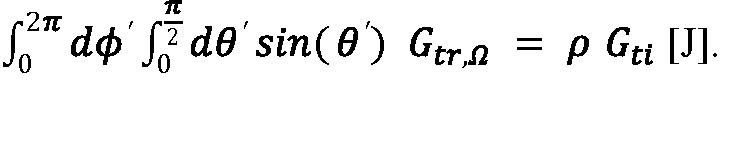
将式9中的θ´设为θ,得到激光雷达系统向系统方向辐射的单位立体角反射能量。考虑大气衰减因素后,反射到激光雷达系统接收孔径的能量为Gtr、Ω与接收孔径所对应的立体角(Ωrx)的乘积,即:
方程11:
Ω处方D =(π24) / (r2) (sr),
其中D为接收孔径的直径,单位为米。
因此,传递给光接收探测器的反射激光脉冲能量为:
方程12:
E处方=η克tr,ΩΩ处方exp (R -σ)[J],
式中η为光学系统的效率。
如果E处方对于不足填充和过度填充的情况,发现了R2相关性(忽略衰减):
方程13:
Erx_UFE =ηρtxD cos(θ)2(exp(2σR)) / (4 R2) [J];
对于过度填充的目标,发现R4依赖关系:
方程14:
Erx_OFE =ηρtx一个t因为2(θ)D2(exp(2σR)) /(4πϕ2R4) [J],
如果R小于R, 13式就适用的,当R大于R时适用式14的.
在公式13和公式14中,当考虑到朗伯反射通常导致各向同性辐射时,保留与公式8相关的cos(θ)因子可能是反直觉的。在被动成像应用中,整个场景被环境光照亮亚博尊贵会员或发射黑体辐射,目标跨越探测器像素的瞬时视场,瞬时视场内的辐射表面积变化为1/cos(θ),抵消了与兰伯反射相关的cos(θ)。这类似于方程5中cos(θ)因子如何抵消入射在未填充的目标表面上的能量,不同的是,在这种情况下,cos(θ)因子影响进入目标的通量是由激光雷达系统在反射之前发射的准直光束照射目标造成的。因此,对于激光雷达系统,有单独的cos(θ)因素,说明方向照明和朗伯反射,在不足填充的情况下,只有一个cos(θ)因素取消由于激光点在目标上的延伸;对于过度填充的情况,不会发生抵消,因为辐射表面积受到目标物理尺寸的限制。
公式3中的阈值信号水平表示为光接收器NEI的倍数(以光子为单位),可以乘以光子能量(焦耳,Eph值),以达到以下的临界值:
方程15:
Erx_th= Nf× nei × eph值[J],
地点:
方程16:
Eph值= (1.9864 × 10-16年) /λ[J],
其中分子以J nm表示,λ为激光波长,单位为nm。
或者,如果光接收器对特定宽度的激光脉冲的灵敏度(TpE的阈值NEP表示处方方形激光脉冲可近似为:
方程17:
Erx_th≈Nf × NEP × Tp[J] .
最大有效范围(R马克斯),可将式13或式14分别代入Erx_th然而,在大气衰减因子exp(-2σR)中R的出现以及在R2和R4式13和式14的分母项不能用初等函数来求解。在衰减可忽略极限下,假设接收机灵敏度为NEI,欠填充目标的最大有效距离为:
方程18:
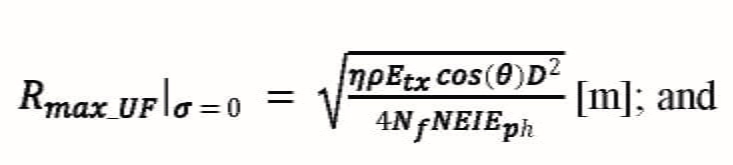
满弹目标的最大有效射程为:
方程19:
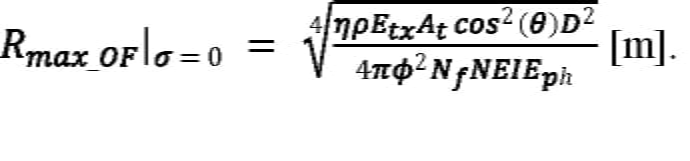
如果计算中包含大气衰减,则解涉及兰伯特W函数的主分支,当W≥-1时,W0[x exp(x)] = x。这个特殊的函数是通过数学软件包(如MATLAB)进行数值计算的lambertw)和Mathematica(其中函数称为ProductLog)。对于未填充的目标情况,一般的解决方案是:
方程20:
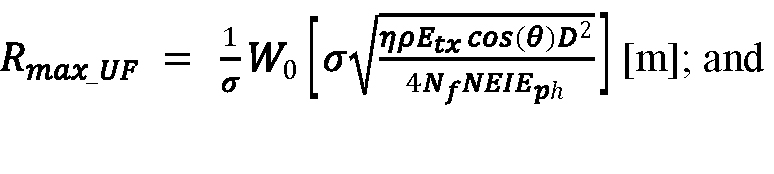
过度填充目标情况的一般解决方案是:
方程21:
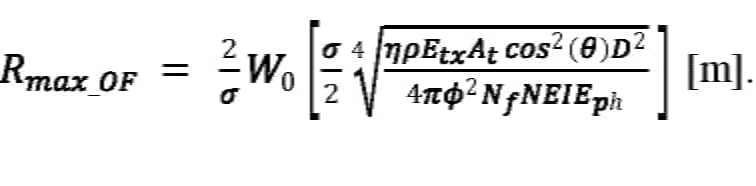
公式18、公式19、公式20和公式21必须谨慎使用,因为目标是不足填充还是过度填充取决于它的范围。用公式18或公式20计算欠填充情况下的最大有效范围可以得到R值马克斯目标被过度填充,因此无效。类似地,基于目标被过度填充的假设,使用公式19或公式21进行计算,可以发现目标实际上未被充分填充的最大有效范围。因此有必要对R进行比较马克斯到ROF,以验证式18、式19、式20和式21的结果。使用实例情况下,有效范围计算在图2中作为不同大气衰减系数对应的条件从可见到轻雾的函数。(这些条件和能见度更有限的条件将在“大气条件”一节中进一步讨论。)
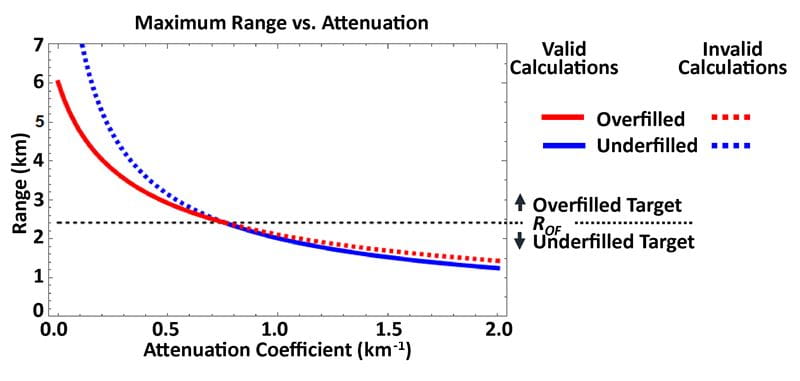
图2:过充和欠充情况下的最大有效范围与大气衰减系数的关系。(过度填充和未充分填充的数据在适用的地方是实线,在不适用的范围是虚线。)
激光脉冲能量与接收光圈
能量传递到激光雷达系统探测器(E处方,以光子表示)在大气衰减系数σ = 0.05 km时的各种传输脉冲能量如图3所示1,相当于23公里的能见度。水平虚线标记S对应的检测阈值th= 3 × NEI和8 × NEI。E的交点处方S形曲线th直线是求最大有效距离的另一种方法。长圆形目标在其短轴上比激光光斑比其长轴宽的点更近的距离上变得过度填充,因此部分过度填充的目标拦截的激光光斑的比例随距离的变化而变化;在这种情况下,式20和式21给出的有效范围的封闭形式表达式不适用,R马克斯必须以图形方式找到,如图3所示,或者使用数值求解器。
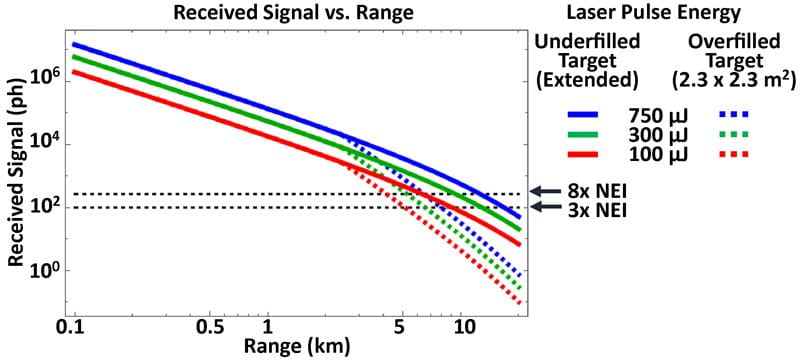
图3:接收信号与不同发射脉冲能量的距离,针对未填充和过填充目标。
图4总结了低填充和过填充目标在不同发射脉冲能量、检测阈值和接收孔径组合下的有效范围。大气衰减系数σ = 0.05 km1假定。
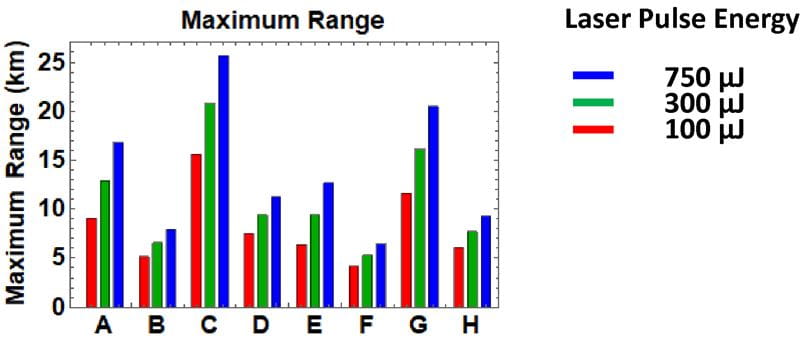
激光雷达和目标参数的有效范围图表
| 年代th= 3 x NEI | 年代th= 8 x NEI | ||||||
| D = 21 mm | D = 50mm | D = 21 mm | D = 50mm | ||||
| 佛罗里达大学 | 的 | 佛罗里达大学 | 的 | 佛罗里达大学 | 的 | 佛罗里达大学 | 的 |
| 一个 | B | C | D | E | F | G | H |
OF =过满目标(目标为2.3 x 2.3 m2)
UF =未填充目标(目标扩展;即大于波束宽度)
图4:各种发射脉冲能量下激光雷达和目标配置的最大范围。
目标反射率
到达目标表面的激光能量部分被吸收,部分被反射。从目标反射的能量是向各个方向散射的漫反射分量(图5,上)和沿反射角等于入射角但与表面法线方向相反的镜面分量的总和(图5,下,最长的出射射线)。显然,激光脉冲能量的吸收部分不能在激光雷达接收机上贡献信号。此外,由于激光雷达系统的光接收机与其激光发射机配置在一起,纯镜面反射只有在完全正入射的特殊情况下或反反射目标的特殊情况下才能到达接收机;这就是激光雷达计算通常假设漫反射的主要原因。
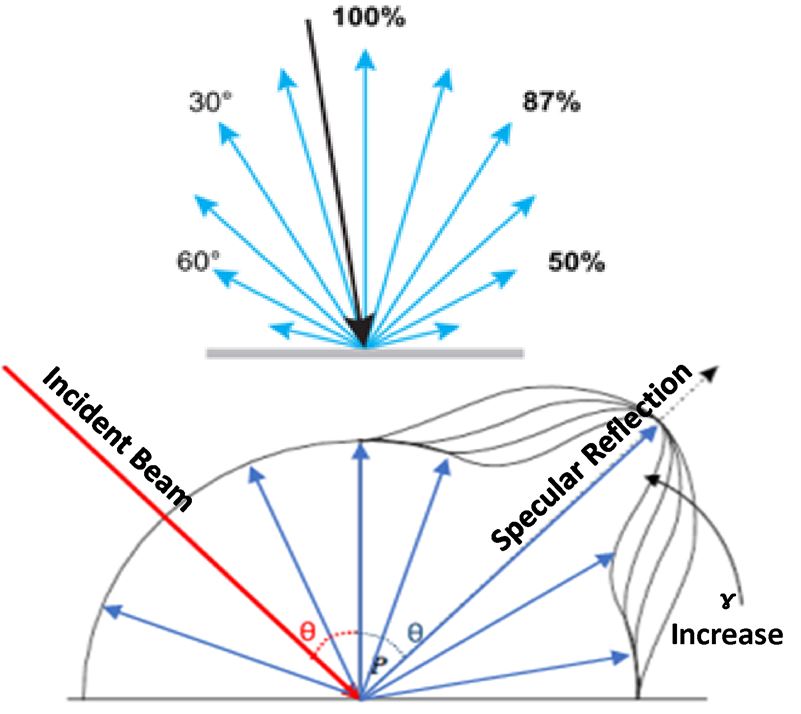
图5:漫反射器(上)和带有漫反射和镜面成分的反射几何(下),其中ɣ为镜面反射率指数。
漫反射的余弦依赖关系已在公式9中给出,用单位立体角的反射能量表示。这是兰伯特余弦定律的一个版本,它更常用辐射强度(Ie,Ω),单位为W sr1.辐射强度的余弦定律为式9除以激光脉冲宽度,将激光脉冲传递的总能量转化为脉冲的平均功率。
假设完美的朗伯反射简化了方程20和方程21,但大多数目标偏离了理想模型。通常,反射率在镜面反射角附近增加。由于其方向依赖性,这一特性被称为高光,但与纯粹的高光反射不同,反射率在高光反射角附近的角度得到增强,而不仅仅是在精确的高光反射角度。由b.t. Phong在1975年开发的用于计算机图形学的现象学模型通过将方程9中的乘积ρ cos(θ′)替换为:
方程22:

其中ρ是前面介绍的漫反射系数,θ′是反射光线与目标表面法线之间的夹角,ρ上海为镜面高光反射率系数,ξ为反射光线与纯镜面反射方向的夹角,ɣ为影响镜面高光角宽度的形状参数。形状对总反射率大小的影响可以在图5底部观察到,其中增加ɣ使高光特征变窄。
将式22代入到式20和式21,其中对于激光雷达系统,后反射光线到激光雷达系统接收机的角度与激光在目标表面的入射角相同,得到θ ' = θ。背反射光线与纯镜面反射方向的夹角ξ = 2θ,因为镜面反射角等于入射角,但与表面法线方向相反。据此,式20、式21可纳入Phong模型,代入:
方程23:
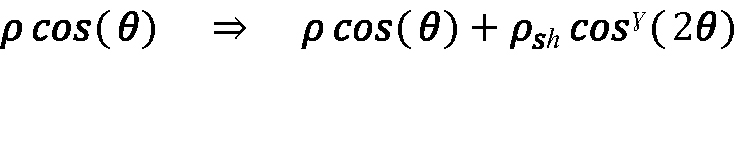
目标表面在正常入射附近的测距比完全正常入射更常见,因此镜面高光引起的反射率增强可能与激光雷达性能有关。然而,由于Phong模型是现象学的,而不是基于第一性原理,因此没有一个通用的理论可以根据基本的材料和表面性质来计算ρsh和ɣ。此外,诸如式20和式21这样的分析模型主要是有用的,因为它们清晰易用。考虑到现实世界目标表面和方向的多样性,像公式23这样的细化会增加模型的复杂性,而不一定会提高模型的精度。实际上,通过考虑激光雷达系统必须在其中工作的最不利的目标假设集以及平均情况,将方程20和方程21等分析模型应用于约束系统性能时是最有用的。通过接近正常入射来提高目标反射率的可能性通常不是最坏的情况,而且就平均情况而言,将镜面高光对反射率的平均提高归结为平均漫反射比明确应用公式23要简单得多。
因为ρ和E成对tx在公式20和式21中,ρ随固定发射激光脉冲能量的变化等价于ρ随固定发射激光脉冲能量的变化。因此,图4所示的100 μJ、300 μJ和750 μJ三种发射激光脉冲能量对30%反射目标的最大有效距离变化也对应于激光能量固定为250 μJ、目标反射率为12%、36%和90%时的最大有效距离性能。一般情况下,式20、式21中分子中根号下的各项-激光脉冲能量、目标反射率、接收机孔径面积、余弦取向因子-之间成比例交易,对有效距离的影响相同。图6绘制了实例目标的最大有效距离,作为各种大气衰减系数的反射率的函数。
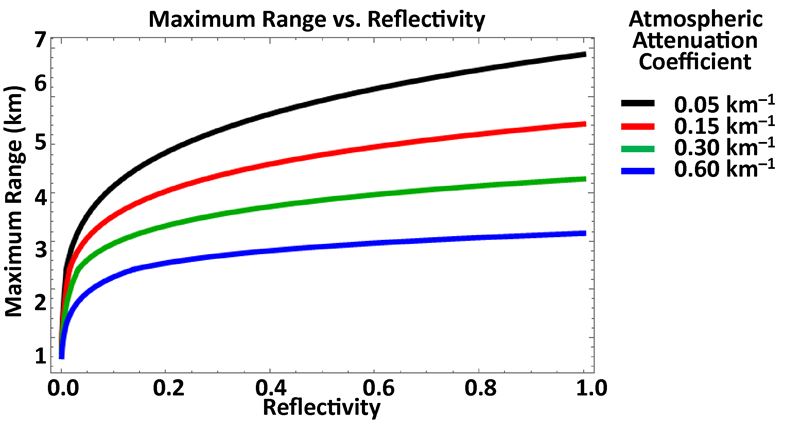
图6:不同大气衰减系数的最大有效距离与反射率系数。
角定位
图7绘制了不同大气衰减系数的最大有效范围与入射角的关系,分别用公式20和公式21计算,反映了欠填和过填情况下不同的θ依赖关系。与目标反射率和镜面高光现象一样,分析目标表面方向的最不利情况和平均情况通常比构建更复杂的分析模型更有用。50.5度的情况导致平均余弦因子的复合目标,其中包括一个更小的方向曲面的集合,均匀分布在θ = 0度和θ = 90度之间。
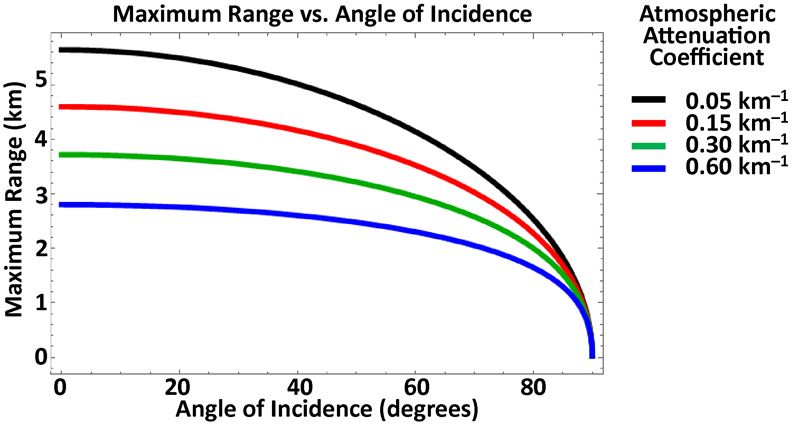
图7:不同大气衰减系数的最大有效距离与入射角。
目标形状
现实世界的目标物体呈现不同区域的多个表面,其特征是反射率和方向角度,这取决于从哪个方面考虑目标。形状不规则的目标在较近的距离上沿较短的横截面轴会比沿较长的轴变得过度填充,并且像树木这样的目标可能会被孔穿孔,激光能量可以通过这些孔而不影响反射信号。因此,基于规则形状单个目标曲面的最大有效距离分析模型(如式20和式21)有助于理解激光雷达性能的物理依赖性,但不能得到普遍适用的结果。基于详细的三维目标模型的数值计算可用于特定的应用,但在分析模型中表示目标复杂性的一种方法是考虑由多个较小的目标表面组成的目标。亚博尊贵会员然后根据表面反射率和入射角的平均值估计激光雷达对典型复杂目标的性能。当这样做时,而不是寻找单独的E值处方对于每个分量表面,将平均反射率降低一个平均余弦因子是可行的。中性假设入射角均匀分布在0和π/2之间,导致平均余弦因子为2/π≈0.637,可以取代方程20和方程21中的cos(θ)。θ = arccos(π/2)≈50.46°可直接用于式20和式21。
大气条件
大气衰减是由分子和气溶胶的散射和吸收造成的。总大气衰减系数是各个过程的系数之和:
方程24:
σ = α米+β米+α一个+β一个[m1),
其中α为吸收系数,β为散射系数,下标m和a分别表示分子过程和气溶胶过程。
短波红外中的分子和气溶胶吸收过程是由组成大气和悬浮粒子的分子的振动激发引起的。分子散射是瑞利散射的另一个术语,而大小与光学波长相当的气溶胶粒子通过Mie过程散射光;由于大气密度的变化,大得多的粒子以及沿光路的折射率波动会根据光学规则散射光。吸收过程非常具有波长选择性,并取决于存在的特定分子种类:而瑞利散射下降为1/λ4, Mie和几何散射强度对波长的依赖性不是很强。
表2以千米为单位显示了各种大气条件下的衰减系数1.注意,这些值必须转换为m1用于本文的方程,这些方程是用SI单位表示的。
表2:衰减系数:各种大气条件
| 衰减系数 | 公里-1(1534海里) |
| 浓雾(能见度0.05公里) | 62.6 |
| 雨 | 10 |
| 轻雾 | 1.00 |
| 中度雾(能见度0.25公里) | 9.71 |
| 何克雾(能见度1公里) | 2.07 |
| 4公里能见度 | 4.61 x10-01年 |
| 海上阴霾 | 7.40 x 10-02年 |
| 阴霾 | 1.50 x 10-02年 |
| 10公里能见度 | 9.21 x 10-02年 |
| 23公里能见度 | 4.61 x 10-02年 |
| 纯净的空气 | 1.00 x 10-02年 |
阳光
由于激光雷达系统只需要响应发射的激光波长,激光雷达系统通常在接收光学器件上有一个窄通带滤波器。同样地,由于激光雷达系统只需要一个足够宽的视场来实际对准投射的激光点,因此从激光雷达系统对目标周围的太阳照明背景的观察是相当有限的。这些因素往往使阳光对激光雷达系统的影响最小化。
用于光伏系统设计的大气质量1.5太阳光谱辐照度为地面太阳背景提供了一个很好的估计。在1534 nm处,地面的太阳光谱辐照度约为Ee,λ= 0.26 W m2纳米1经过1.5倍天顶路径长度穿过大气层后。假设背景是一个以忽略ρ的大气衰减和光学效率损失为特征的朗伯反射面,激光雷达探测器上的通量为:
方程25:
Φe= π/16 ee,λΔλρω2D2[W],
其中Δλ为滤波器带通,单位为nm, ω为激光雷达视场角,单位为弧度。对于Δλ = 10 nm, ρ = 30%, ω = 10 mrad, D = 50 mm,探测器上的通量约为38 nW。产生的背景光电流是Φ的产物e探测器响应度约为1a W1对于InGaAs光电二极管和工作在雪崩增益M的InGaAs APD大M倍。
背景光电流与探测器的暗电流具有相同的噪声影响;因此,如果背景光电流的大小与探测器暗电流相似,它可能会影响基于APD的激光雷达系统的灵敏度,这取决于APD的增益工作点相对于其放大器电路的噪声。相反,如果背景光电流比探测器暗电流小一个数量级以上,其对激光雷达灵敏度的影响可以忽略不计。同样,暗电流和背景光电流通常都不会影响基于光电二极管的激光雷达电路的灵敏度,它们的灵敏度低于基于apd的激光雷达系统,主要受放大器噪声的影响。
当测距目标与太阳盘的角分离很小时,来自接收阳光的背景光电流的增加可能会在固定的探测阈值下潜在地增加FAR。计算背景光电流对激光雷达系统的影响需要前面讨论过的分析方法。但在一般情况下,当背景光电流上的射击噪声变得明显时,必须提高激光雷达系统的检测阈值以降低远距;因此,年代th必须增加,减少激光雷达系统的最大有效距离。
折射率变化
由于距离是根据光脉冲穿过激光雷达系统和目标之间路径的速度计算的,因此距离精度取决于知道该路径中大气的平均群折射率,这取决于大气的折射率及其在激光波长附近的色散。光脉冲在真空中的群速度与其相速度相同,c = 299,792,458 m s1;而且,当激光脉冲穿过空气等介质时,其速度会因群折射率而降低。空气折射率作为波长、空气温度、大气压力、湿度和二氧化碳含量的函数计算的通用模型已经发表,其中两个已由NIST作为基于web的计算器实现。[1]
空气的折射率-在平均海平面压力下20°C,相对湿度50%,450 ppm CO2分压为1.000268148。此值可用于基线计算。然而,由于激光脉冲的飞行时间取决于沿光路的平均传播速度,较长距离测量的精度受到未校正的群折射率误差的影响。未校正的平均折射率误差(Δn)导致距离测量误差(ΔR),与实际距离成正比:
26个方程:
ΔR = Δn R [m]. .
微小的环境变化——比如1摄氏度的温度变化或0.4千帕的气压变化——都可能导致折射率高达百万分之一的变化。
最后,如“大气条件”一节所述,折射率沿激光雷达系统和目标之间光路的空间波动可以散射和重定向传播的激光脉冲。这些折射率波动除了有助于衰减外,还会引导激光脉冲偏离激光雷达系统与目标之间的直线路径,影响距离测量。与距离误差一样,衰减和失真的严重程度随着目标距离的增加而增加。
[1]见https://emtoolbox.nist.gov/Wavelength/Abstract.asp。2018年11月8日
